空间金字塔池化（SPP）关键参数计算

发布于：2022-07-03 | 分类：mathematics , machine learning

空间金字塔池化（Spatial Pyramid Pooling）方法关联了不定尺寸输出的卷积层和固定大小的全连接层，一方面可以适应不同尺寸图片输入，避免了统一图片大小的前处理操作；另一方面可以提取不同尺寸的空间特征信息，进而提升模型对于空间布局和物体变形的鲁棒性。SPP的基本原理请参考原论文或相关解读，本文基于输入输出尺寸，分析SPP关键参数例如窗口尺寸（kernel）、步长（stride）及边距（padding）的计算方法。

问题提出

已知卷积后输出尺寸 (w, h)，空间金字塔池化后目标输出 (n_w, n_h)，计算池化层的窗口尺寸(k_w, k_h)，步长(s_w, s_h)及边距(p_w, p_h)。为了简化描述，以下仅基于其中一个维度计算，另一维度采用完全相同的计算公式。因此，相应参数简化为：

已知输入、输出尺寸w和n，求池化窗口尺寸(k)，步长(s)及边距(p)。

如果正向计算，公式为：

n = \left \lfloor \frac {w+2p-k} {s} \right \rfloor + 1 \tag{1}

其中 \lfloor x \rfloor 表示对x向下取整，例如 \lfloor 1.5 \rfloor = 1，同理向上取整符号及例子：\lceil 1.5 \rceil = 2。

原始论文公式

原论文中的计算公式：

k = \left \lceil \frac {w} {n} \right \rceil, \quad s = \left \lfloor \frac {w} {n} \right \rfloor, \quad p = 0 \tag{2}

有些解读论文的博文指出了问题及反例：

取 w=7, n=4，根据公式（2）得出 k=2,s=1,p=0，

然而将池化参数带入公式（1）却得出矛盾的结果：n=5！

注意：

这是作者为论文中特定场景提出的，确实并不具备（作者也没主张）其通用性。

初步修正的公式

参考博文，给出了如下通用性更好的公式：

k = s = \left \lceil \frac {w} {n} \right \rceil \\\\ p = \left \lfloor \frac {k*n-w+1} {2} \right \rfloor \tag{3}

对上一个例子 w=7, n=4，根据公式（3）可以得出正确结果： k=2,s=2,p=1。

但还是可以找到有问题的例子：

取 w=5, n=4，根据公式（3）得出 k=2,s=2,p=2，

带入公式（1）验证没问题，但是 pytorch要求 padding 不超过 kernel 的一半 即 k >= 2p，显然此处不满足。

可行域分析

为了方便分析这个问题，先排除两种特殊情况：

  • 当 n>w 时，不符合SPP的物理意义

  • 当 n=1 即输出为1时，取窗口正好为输入尺寸：k=w, s=1, p=0

于是在 w \geq n \gt 1 条件下，列出以下限制条件/不等式：

(n-1)*s+k-w \leq 2p \lt n*s+k-w \tag{4-1}
0 \leq 2p \leq k \tag{4-2}
1 \leq s \leq k \leq w \tag{4-3}
(n-1)*s+k \geq w + p \tag{4-4}

其中，

  • 不等式（4-1）直接从等式（1）去掉取整符号得到；
  • 不等式（4-2）避免引入过多无意义的边距信息，也是 pytorch 中的一个限制；
  • 不等式（4-3）要求步长不大于窗口大小，否则跳过了有效区域；
  • 不等式（4-4）左边表示池化操作的实际作用范围，右边表示特征图的有效位置，因此整个式子要求池化操作覆盖所有有效区域。

将不等式（4-1）左半部分取整得到 p 的计算公式：

p = \left \lceil \frac {(n-1)*s + k - w} {2} \right \rceil \tag{5}

将 k=s 代入上式即可得到公式（3）中计算 p 的部分，表明上式更具一般性，公式（3）计算 p 的方法只是公式（5）一个特例。

结合（4-1）左半部分和（4-2）右半部分：

k \geq 2p \geq (n-1)*s+k-w => s \leq \frac {w} {n-1}

结合（4-1）右半部分和（4-3）：

0 \leq 2p \lt n*s+k-w \leq n*k+k-w => k \gt \frac {w} {n+1}

不等式（4-4）缩放一下去掉 p：

(n-1)*s+k \geq w

综合得到：

\begin{cases} 1 \leq s \leq \frac {w} {n-1} \\\\ \frac {w} {n+1} \lt k \leq w \\\\ k \geq s \\\\ k \geq (1-n)*s + w \end{cases} \tag{6}

注意各个参数都是非负整数，但此刻先不做区分，直接线性规划求解可行域，得到下图。

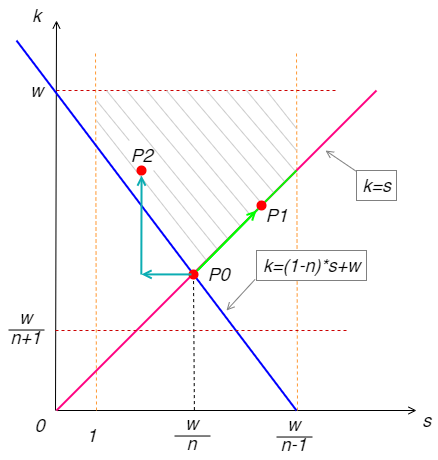
general-flow

显然，解可能不唯一。我们先得到一个特征点 P_0(w/n, w/n)，然后基于不同的策略有不同的选择：

  • 如果沿着绿色箭头方向往 P_1 方向走，窗口大小始终与步长相等，即传统的池化模式。

  • 如果沿着青色箭头方向往 P_2方向走，窗口大小始终大于步长，即带重叠模式的池化。

以 P_1 方向为例，因为 k,s 都是正整数，我们取 P_0 右侧最接近的正整数值，即 k = s = \lceil w / n \rceil ，于是得到了网上常见的初步修正的公式，即上文的公式（3）。

至此，可以统一上文提及的计算方法，并且完美解释以下两个问题：

（a）公式（3）在什么情况下不再适用？

对照可行域图就很好解释了——绿色线段上可能不存在整数解。

例如例子中 w=5,n=4，绿色线段两个端点的 s 坐标分别为 1.25 和 1.667，二者之间并不存在正整数。

那么，公式（3）在什么条件下才适用呢？令 w=a*n+b，其中 0 \leq b \lt n，则

\frac {w} {n-1} = \frac {a*n+b} {n-1} = a + \frac {a+b} {n-1}

显然，w/(n-1) 的整数部分至少达到 a+1 即 (a+b)/(n-1) \geq 1 时，绿色线段标注的可行域上才有整数解：

\left \lfloor \frac {w} {n} \right \rfloor + \left(w \mod n\right) + 1 \geq n

进一步考虑端点上的情况，即上式取等号，此时 w/(n-1) 恰好为整数，且 k=s=w/(n-1)，参考公式（5）可知：

p = \left \lceil \frac {n*k - w} {2} \right \rceil = \left \lceil \frac {w} {2 *(n-1)} \right \rceil = \left \lceil \frac {k} {2} \right \rceil

结合 k \geq 2p 的限定条件，此时要求 k 即 w/(n-1) 必须为偶数。

综上，公式（3）的使用条件：

t = \left \lfloor \frac {w} {n} \right \rfloor + \left(w \mod n\right) + 1
t \gt n \quad \lor \quad \left( t = n \quad \land \quad w/(n-1) \mod 2 = 0 \right) \tag{7}

其中，\lor 和 \land 分别表示“或”和“且”。

（b）如何处理公式（3）不适用的情况？

当 w,n 不满足不等式（7）时，公式（3）失效，那就走 P_2 的路线，如青色箭头所示：

  • 此种情况下往右显然不存在可行的s了，于是向左一步得到 P_0 附近的 s；

  • 然后向上增大 k 直到满足可行域要求。

以上过程反映了公式（2）的思路，但是为了更具通用性，确定 k 时需要检查是否落在可行域内。将公式（2）中 s 的表达式代入（4-4）的缩放式得到 k，然后将 k,s 代入公式（5）计算 p，最终得到公式（2）的更一般形式：

s = \left \lfloor \frac {w} {n} \right \rfloor, \quad k = w - (n-1)*s, \quad p = 0 \tag{8}

回到 w=5,n=4 的例子，代入上式得到 k=2, s=1, p=0，满足所有约束。

注意：

上式和公式（2）的最直接区别是 k 的计算方法。公式（2）在定义 k,s 的同时强行设定 p=0（或者说忽略了 p 的计算），实际上三者是相互关联的。公式（8）通过构造 k，使 p=0 自然得到满足。

完整算法

已知输入、输出尺寸 w 和 n（w \geq n），求SPP池化层的窗口尺寸(k)，步长(s)及边距(p)。

（1）当满足不等式（7）时，

s = k = \left \lceil \frac {w} {n} \right \rceil, \quad p = \left \lceil \frac {n*k - w} {2} \right \rceil

（2）当不满足不等式（7）时，

s = \left \lfloor \frac {w} {n} \right \rfloor, \quad k = w - (n-1)*s, \quad p = 0

注意：以上算法优先选择传统非重叠的池化方式，只有在无法满足时，才考虑重叠的池化方式。如果倾向于重叠的池化方式，则直接选择第（2）部分计算公式即可。